Question

Solve the system of linear equations using matrices.4y-z=-5X+ 5y +z=-32x-y + 3z =13

Answer 1

The given system expressed as a matrix would be

0 4 -1 -5

1 5 1 -3

2 -1 3 13

To solve this, first, we have to change the first row for the second

1 5 1 -3

0 4 -1 -5

2 -1 3 13

Now, we multiply the first row by 2, then subtract it from the third row.

1 5 1 -3

0 4 -1 -5

0 -11 1 19

Then, we multiple the second row with -11/4 to subtract it from the third row.

1 5 1 -3

0 4 -1 -5

0 0 -7/4 21/4

The resulting system would be

`\mleft\{\begin{aligned}x+5y+z=-3 \\ 4y-z=-5 \\ -(7)/(4)z=(21)/(4)\end{aligned}\mright.`

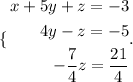
We solve for z

`\begin{gathered} (-7)/(4)z=(21)/(4) \\ z=(21)/(-7)=-3 \end{gathered}`

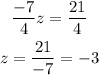
Therefore, z is equal to -3.

We use z to find y in the second equation.

`\begin{gathered} 4y-(-3)=-5 \\ 4y+3=-5 \\ 4y=-5-3 \\ 4y=-8 \\ y=(-8)/(4)=-2 \end{gathered}`

Therefore, y is equal to -2.

We use y and z to find x in the first equation.

`\begin{gathered} x+5(-2)+(-3)=-3 \\ x-10-3=-3 \\ x=-3+10+3=10 \end{gathered}`

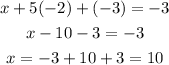
Therefore, x is equal to 10.