Question

how do I know what exponent and base I use when I simplify an exponent, for example, 16^1/4 become (2^4)^1/4 which becomes 2. How do I know I have to use 2^4 instead of another number like 4^2 that is still equal to 16. Why can't I use a different number that is equal to the same thing?

Answer 1

Reason:

16^1/4=(2^4)^1/4

Step-by-step explanation:

You can use either 4^2 or 2^4 both gives the same answer.

In order to simplify the steps we use 2^4.

we get,

`16^{(1)/(4)^{}^{}}=(2^4)^{(1)/(4)}`
`=2^{4*(1)/(4)}`

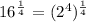
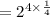
4 in the power got cancelled and we get,

`=2`

Alternate method:

If we use 4^2 we get,

`16^{(1)/(4)}=(4^2)^{(1)/(4)}`
`=4^{2*(1)/(4)}`
`=4^{(1)/(2)}`

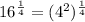
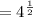
we use 4=2^2,

`=(2^2)^{(1)/(2)}=2`

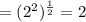
In order to get answer quicker we appropiately use 2^4=16 here.

Rules in exponent:

`a^n* a^m=a^(n+m)`
`(a^n)/(a^m)=a^(n-m)`
`(1)/(a^m)=a^(-m)`
`(a^n)^m=a^(n* m)`
`4^{3*(1)/(2)}=4^{(3)/(2)}`

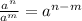
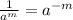
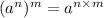
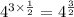
use 4=2^2, we get

`=2^{2*(3)/(2)}`

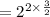
2 got cancelled in the power, we get

`=2^3`
`=8`

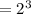
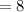
we get,

`4^{3*(1)/(2)}=8`