Given the image in the question, it can be seen that the roof forms a right angled triangle. Therefore, we can get the length of the roof rafters (x) by using the Pythagoras theorem.
Step 1: We define the Pythagoras theorem and state our parameters
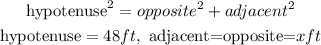
Step 2: We substitute the values into the theorem to solve for x
![\begin{gathered} 48^2=x^2+x^2 \\ 2x^2=2304 \\ x^2=(2304)/(2) \\ x^2=1152 \\ x=\sqrt[2]{1152} \\ x=33.9411255 \\ x\approx33.94ft \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/f7b9ds4ibbt5o73vzgw6.png)
Hence, the length of the roof rafters (x) is 33.94ft to the nearest hundredth.