Question

Options for the first box are: One valid solution, two valid solutions Options for the second box are: no extraneous solutions, one extraneous solution Options for the third box: 5, 0, 2, 4

Answer 1

The equation has one valid solution and one extraneous solution.

A valid solution for x is 5

`\sqrt[]{x-1}-5=x-8`

Add 5 to both-side of the equation

`\sqrt[]{x-1}-5+5=x-8+5`
`\sqrt[]{x-1}=x-3`

Take the square of both-side

`x-1=(x-3)^2`

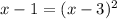
x - 1=x²-6x + 9

Rearrange

x² - 6x + 9 - x + 1 =0

x² - 7x + 10 = 0

We can solve the above quadratic equation using factorization method

x² - 5x - 2x + 10 = 0

x(x-5) - 2(x - 5) = 0

(x-5)(x-2)=0

Either x -5 =0 OR x-2 =0

Either x =5 or x=2

To check whether the equation is valid or non-extraneous, let's plug the values into the equation and see if it gives a true statement

For x =5

`\sqrt[]{5-1}-5=5-8`

`\sqrt[]{4}-5=-3`
`-3=-3`

The above is a true statement

For x =2

`\sqrt[]{2-1}-5=2-8`
`1-5=2-8`

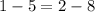
The above is not a true statement

Therefore, the equation has one valid solution and one extraneous solution.

A valid solution for x is 5