Question

find the upper and lower sums for the region bounded by the graph of the function and the x-axis on the given interval. Leave your answer in terms of n, the number of subintervals.

Answer 1

Step-by-step explanation

The area under a curve between two points can be found by doing a definite integral between the two points

Step 1

a) set the intergral

`\begin{gathered} limits:\text{ 1 and 2} \\ function:\text{ f\lparen x\rparen=6-2x} \end{gathered}`

hence

`Area=\int_1^26-2x`

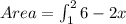
Step 2

evaluate

let ; numbers of intervals

`\begin{gathered} \begin{equation*} \int_1^26-2x \end{equation*} \\ \int_1^26-2x=\lbrack6x-x^2\rbrack=(12-4)-(6-1)=8-5=3 \end{gathered}`

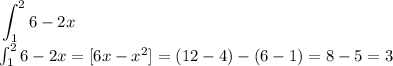
therefore, the area is

`area=3\text{ units }^2`

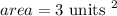
I hope this helps you