Question

PRECALC QUESTION!!!!!!

Answer 1

$21.50

Explanation:

The given function, which describes the monthly profit f(p) as a function of the price of a picture frame (p), is a quadratic equation. Its negative leading coefficient indicates that it is a downward-opening parabola.

The vertex of a downward-opening parabola is the point at which the parabolic curve reaches its maximum value. Therefore, to identify the price of a frame (p) that maximizes the profit, we need to locate the x-coordinate of the vertex of this quadratic function.

The formula for the x-coordinate of the vertex of a quadratic equation in the form y = ax² + bx + c is:

`\boxed{x=(-b)/(2a)}`

In the case of f(p) = -80p² + 3440p - 36000:

• a = -80
• b = 3440
• c = 36000

Substitute the values of a and b into the vertex formula:

`x=(-3440)/(2(-80))`

`x=(-3440)/(-160)`

`x=21.50`

Therefore, the price per frame that generates the maximum profit is $21.50.

Answer 2

Price that generates maximum profit= $21.50

Maximum profit = $980

Explanation:

To find the price that generates the maximum profit, we need to find the maximum point of the function $f(p)$. The maximum point of a quadratic function is located at the vertex of the parabola.

The vertex of a parabola can be found using the formula
`\sf x=-(b)/(2a)`, where a and b are the coefficients of the x² and x terms in the quadratic equation, respectively.

In the case of the function f(p),

Comparing with f(p) = ax² + bx + c,

we get a=-80 and b=3440 and c = -36,000.

Substituting these values into the formula, we get:

`\sf x=-(b)/(2a)=-(3440)/(2(-80))=21.50`

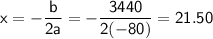
This means that the maximum profit is generated when the price per frame is $21.50.

We can also find the maximum profit by evaluating the function at its vertex.

Evaluating f(p) at p=21.50, we get:

f(21.50)=-80(21.50)²+3440(21.50)-36,000

= -80 × 462.25 + 73960 - 36,000

= −36980 + 73960 - 36,000

= 980

Therefore, the maximum profit is $980 and it is generated when the price per frame is $21.50.