Question

What is a formula that can be used to find the area of one triangular section of the door how do you know the formula will work?

Answer 1

`Area = (1)/(2) L B`

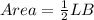
Explanation:

Given

See attachment for complete question

Required

Determine the formula of one of the triangular sections

From the attachment, we have that:

`L = Length`

`B = Height`

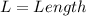
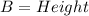
The area of the triangle is:

`Area = (1)/(2) * L * B`

`Area = (1)/(2) L B`

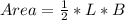
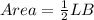
How to know the formula works?

From the attachment, we can see that the rectangle is divided into two equal triangular sections.

The area of the rectangle is:

`Area = L* B`

`Area = LB`

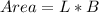
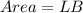
Because the rectangle is divided into two equal triangular sections.

This implies that, the area of one of the triangular sections is half the area of the rectangle.

So:

`Area(Triangle) = (1)/(2)Area(Rectangle)`

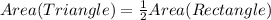
Substitute LB for the area of the rectangle

`Area(Triangle) = (1)/(2)LB`

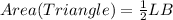
By comparison:

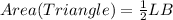`Area(Triangle) = (1)/(2)LB` and
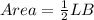`Area = (1)/(2) L B` are the same