Given:
Required:
We need to answer the questions
Step-by-step explanation:
Angle LMN and angle PON are the congruent because both are alternate angles
Now angle LNM and angle ONP are also congruent because those two triamgles are similar and both are internal angles
Now to find the value of x
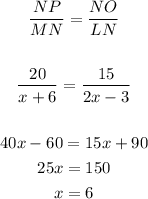
Final answer:
x=6