I'll do problem 1 to get you started.
The answer to problem 1 is 3400 miles
============================================================
Explanation for problem 1:
We're asked to find the perimeter, which is the total distance around the exterior or outside. In other words, we need to add up the four side lengths of this quadrilateral.
We'll need the distance formula to find the lengths of the slanted sides AB and BC
----------------------------------------
Let's first find the length of segment AB
A = (x1,y1) = (0,0)
B = (x2,y2) = (400,300)
d = Length of AB

The distance from A to B is 500 miles. This is the same as saying segment AB is 500 miles long.
----------------------------------------
Now find the length of segment BC
B = (x1,y1) = (400,300)
C = (x2,y2) = (-800,800)
d = length of BC
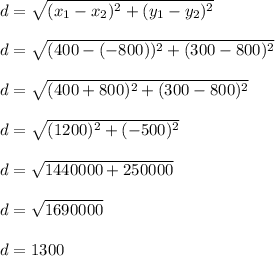
----------------------------------------
The length of CD is fairly easy to find without needing the distance formula. This is because it is a vertical line. We subtract the y coordinates of C and D to get 800-0 = 800. So CD is 800 miles long.
Segment DA is a similar story. But we subtract the x coordinates. This only works for horizontal lines. DA is 800 miles long because |-800-0| = 800. Absolute value is used to make sure the distance is never negative.
----------------------------------------
To summarize everything so far, we found these four side lengths
- AB = 500
- BC = 1300
- CD = 800
- DA = 800
The perimeter is going to be the sum of those four sides, leading to...
perimeter = sum of sides
perimeter = AB+BC+CD+DA
perimeter = 500+1300+800+800
perimeter = 3400 miles
This is the total distance traveled if you started at city A, went to B, then to C, then to D, and then finally went back to A.