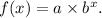Question

If f(x) is an exponential function where f(-0.5) = 28 and f(8.5) = 88, then find the value of f(1.5), to the nearest hundredth.

Answer 1

To find the value of f(1.5) for an exponential function, we can use given points to form the equation and solve for the unknown variables. Then, substitute the value of x = 1.5 into the equation to calculate f(1.5).

Step-by-step explanation:

To find the value of f(1.5), we need to determine the equation of the exponential function. We already have two points on the graph: f(-0.5) = 28 and f(8.5) = 88. Using these points, we can form the equation
`f(x) = a * b^x`, where a is the initial value of the function and b is the growth factor.

Using the point (-0.5, 28), we substitute these values into the equation to solve for a:

`28 = a * b^{(-0.5)`

Next, using the point (8.5, 88), we substitute these values into the equation:

`88 = a * b^{(8.5)`

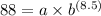
Solving these two equations simultaneously will give us the values of a and b. Once we have these values, we can calculate f(1.5) by plugging x = 1.5 into the equation
`f(x) = a * b^x.`

Answer 2

The exponential function is
`\text{f(x)} = 30 * 1.14^x` and the value of f(1.5) is 36.5

How to determine the exponential function

From the question, we have the following parameters that can be used in our computation:

f(-0.5) = 28

f(8.5) = 88

An exponential function is represented as

`\text{f(x)} = ab^x`

Using the points, we have

`ab^(-0.5) = 28`

`ab^(8.5) = 88`

Divide the functions

So, we have

`(ab^(8.5))/(ab^(-0.5)) = (88)/(28)`

Evaluate

`b^9 = 3.143`

Take the 9th root of both sides

b = 1.14

Recall that

`ab^(-0.5) = 28`

So, we have

`a * 1.14^(-0.5) = 28`

a * 0.94 = 28

Divide

a = 30

This means that

`\text{f(x)} = 30 * 1.14^x`

When x = 1.5, we have

`\text{f(1.5)} = 30 * 1.14^{1.5`

Evaluate

`\text{f(1.5)} = 36.5`

Hence, the exponential function is
`\text{f(x)} = 30 * 1.14^x` and the value of f(1.5) is 36.5