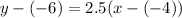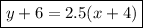Question

What is an equation of the line that passes through the point (−4,−6) and is parallel to the line 5x−2y=2?

Answer 1

`y + 6=2.5(x+4)`

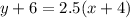
Explanation:

First, we can identify the slope of the line by converting the line it is supposed to be parallel to into slope-intercept form:

`5x-2y=2`

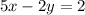
↓ adding 2y to both sides

`5x = 2y + 2`

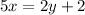
↓ subtracting 2 from both sides

`5x - 2 = 2y`

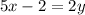
↓ dividing both sides by 2

`\boxed{(5)/(2)}\,x-1=y`

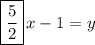
Now, the equation is in the form:

`y=mx+b`

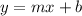
where
`m` is the line's slope.

So, we can identify the slope as 5/2 or 2.5.

Next, we can plug this slope value into the point-slope form of a linear equation:

`y - b = m(x-a)`

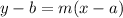
where the line goes through
`(a,b)` and its slope is
`m`:

`y - b = 2.5(x-a)`

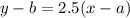
We can set the following variable values from the given point
`(-4,-6)`:

• 
  `a=-4`
• 
  `b=-6`

Finally, we can plug these into the point-slope form equation to get the equation of the line that goes through
`(-4, -6)` and is parallel to
`5x - 2y = 2`:

`y - (-6) = 2.5(x-(-4))`

`\boxed{y + 6=2.5(x+4)}`