Question

In ΔSTU, u = 3.6 inches, s = 7.9 inches and ∠T=68°. Find the length of t, to the nearest 10th of an inch.

Answer 1

7.4 inches

Explanation:

The law of cosines is a trigonometric formula used to find the length of an unknown side of a triangle when the lengths of the other two sides and the included angle are known.

To find the length of side t in triangle STU, we can the law of cosines because we have been given the lengths of two of the sides (u and s) and the included angle (∠T).

The law of cosines states that in a triangle ABC:

`\boxed{c^2= a^2 + b^2 - 2ab \cos(C)}`

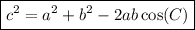
where a, b and c are the sides, and C is the angle opposite side c.

Relating this to the original question, we can rewrite it as:

`t^2= u^2 + s^2 - 2us \cos(T)`

Substitute the given values of u, s, and T into the formula and solve for t:

`t^2= (3.6)^2 + (7.9)^2 - 2(3.6)(7.9) \cos(68^(\circ))`

`t^2= 12.96 + 62.41 - 56.88 \cos(68^(\circ))`

`t^2= 75.37 - 56.88 \cos(68^(\circ))`

`t= \sqrt{75.37 - 56.88 \cos(68^(\circ))}`

`t=7.35271221839...`

`t=7.4\; \sf inches\;(nearest\;tenth)`

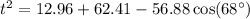
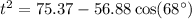
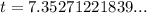
Therefore, the length of side t is 7.4 inches (rounded to the nearest tenth of an inch).