Question

Find the compound interest principal 10,000 interest rate 0.5 time 2 years​

Answer 1

$100.25

Explanation:

To find the compound interest, we can use the compound interest formula:

`\sf I = P \left(\left(1 + (r)/(n)\right)^(nt) -1\right)`

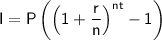
Where:

• I is the compound interest
• P is the principal amount (the initial amount of money) - $10,000 in this case.
• r is the annual interest rate (in decimal form) - 0.5% should be converted to 0.005.
• n is the number of times that interest is compounded per year.
• t is the number of years.

In this case, we have:

• P = $10,000
• r = 0.5% = 0.005 in decimal
• n = 1 (compounded annually)
• t = 2 years

Now, we can substitute these values into the formula to calculate the compound interest:

`\begin{aligned} \textsf{ Compound Interest} & = 10,000 \left(\left(1 + (0.005)/(1)\right)^(1 \cdot 2) -1\right) \\\\ & = 10,000\left( \left(1 + 0.005\right)^2 - 1\right) \\\\ & = 10,000 \left((1.005)^2-1\right) \\\\ &= 10,000 (1.010025-1) \\\\ &= 10,000 \cdot 0.010025 \\\\ &= 100.25 \end{aligned}`

So, the compound interest on a $10,000 principal with a 0.5% annual interest rate compounded over 2 years is $100.25.