Question

3.) Solve each triangle

Answer 1

Part a):

• m∠X = 76°
• m∠Y = 72°
• m∠Z = 32°
• XY = 12 cm
• YZ = 22.0 cm
• XZ = 21.5 cm

Part b):

• m∠D = 60.4°
• m∠E = 36.6°
• m∠F = 83°
• DE = 25 cm
• EF = 21.9 cm
• DF = 15 cm

Explanation:

To solve a triangle, we need to find the measures of all three interior angles and the lengths of all three sides of the triangle.

`\hrulefill`

Part a)

Use the fact that the interior angles of a triangle sum to 180° to determine the measure of angle X:

`\begin{aligned}m\angle X + m\angle Y + m\angle Z & = 180^(\circ)\\m\angle X + 72^(\circ) + 32^(\circ) & = 180^(\circ)\\m\angle X + 104^(\circ) & = 180^(\circ)\\m\angle X &=76^(\circ)\end{aligned}`

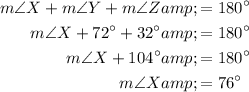
To find the lengths of the sides of the triangle XYZ, we can use the Sine Rule:

`(YZ)/(\sin X)=(XZ)/(\sin Y)=(XY)/(\sin Z)`

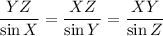
Substitute the known values:

`(YZ)/(\sin 76^(\circ))=(XZ)/(\sin 72^(\circ))=(12)/(\sin 32^(\circ))`

Solve for side YZ:

`(YZ)/(\sin 76^(\circ))=(12)/(\sin 32^(\circ))`

`YZ=(12\sin 76^(\circ))/(\sin 32^(\circ))`

`YZ=21.9723069...`

`YZ=22.0\; \sf cm\;(nearest\;tenth)`

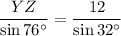
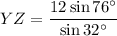
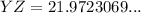
Solve for side XZ:

`(XZ)/(\sin 72^(\circ))=(12)/(\sin 32^(\circ))`

`XZ=(12\sin 72^(\circ))/(\sin 32^(\circ))`

`XZ=21.5366357...`

`XZ=21.5\; \sf cm\;(nearest\;tenth)`

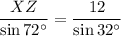
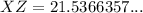
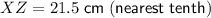
Therefore:

• m∠X = 76°
• m∠Y = 72°
• m∠Z = 32°
• XY = 12 cm
• YZ = 22.0 cm
• XZ = 21.5 cm

`\hrulefill`

Part b)

To find the measures of the angles and lengths of the sides of the triangle DEF, we can use the Sine Rule:

`(EF)/(\sin D)=(DF)/(\sin E)=(DE)/(\sin F)`

Substitute the known values:

`(EF)/(\sin D)=(15)/(\sin E)=(25)/(\sin 83^(\circ))`

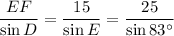
Solve for angle E:

`(15)/(\sin E)=(25)/(\sin 83^(\circ))`

`15=(25\sin E)/(\sin 83^(\circ))`

`\sin E=(15\sin 83^(\circ))/(25)`

`E=\sin^(-1)\left((15\sin 83^(\circ))/(25)\right)`

`E=36.55025914...^(\circ)`

`E=36.6^(\circ)\; \sf (nearest\;tenth)`

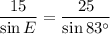
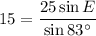
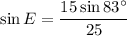
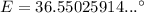
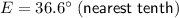
Use the fact that the interior angles of a triangle sum to 180° to determine the measure of angle D:

`\begin{aligned}m\angle D + m\angle E + m\angle F & = 180^(\circ)\\m\angle D + 36.55025914...^(\circ) + 83^(\circ) & = 180^(\circ)\\m\angle D + 119.55025914...^(\circ) & = 180^(\circ)\\m\angle D &=60.4497408...^(\circ)\\m\angle D&=60.4^(\circ)\end{aligned}`

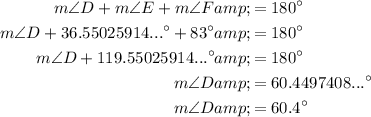
Now, use the Sine Rule again to find the length of side EF:

`(EF)/(\sin \left(60.4497408...^(\circ)\right))=(25)/(\sin 83^(\circ))`

`EF=(25\sin \left(60.4497408...^(\circ)\right))/(\sin 83^(\circ))`

`EF=21.9114096...`

`EF=21.9\;\sf cm\;(nearest\;tenth)`

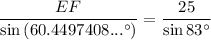
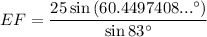
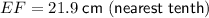
Therefore:

• m∠D = 60.4°
• m∠E = 36.6°
• m∠F = 83°
• DE = 25 cm
• EF = 21.9 cm
• DF = 15 cm