Answer:
a.)

b.)

c.)

d.)
 and
and
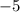
e.)
 and
and

f.)

g.) D: (-∞,∞)
f.) R: [-2,∞)
Step-by-step explanation:
The graph is really helpful to solve these problems. Let me explain how to do each part.
a. For a, we are asked to find f(0) and we are given the function f(x). f(x) just represents the whole function while f(0) represents the y-value of the function when you plug in 0 for x. Look at the graph and find where x=0, and you will see that the y-value is 6.
b. For b, we are asked to find f(-1). Let's use the same procedure as part a. We need to locate the y-value for when we plug in x, and if you go to -1 in the x-axis, the resulting y-value is 4.
c. For c, we are asked to find f(1). Same thing, use the steps we took in an and b to solve. All we must do is locate the y-value when we plug in x, and if you go to 1 on the x-axis, the resulting y-value is 8.
d. For d, we are asked to find the values of x when f(x) = 0. This is a little more tricky. We are used to dealing with graphs where we need to find the x-intercepts of graphs, and setting a functions to 0 has the same implication. All we have to do is locate the x-values when y = 0, and we see that -3, and -5 are the values.
e. For e, all we must do is write the coordinate pairs of the values we got in part d. Therefore, it will just be (-3,0) and (-5,0).
f. For f, we just need to use our answer for part a and write it in coordinate form. Therefore, it will just be (0,6).
g. To find the domain, we must see all the possible/allowed x-values of the function. This looks to be an absolute value function, and with the graph, we notice no restriction on the possible x values. All values are allowed. Therefore, the domain is (-∞,∞).
h. Lastly, we must find the range. The graph is how you are able to solve this. If you look at the vertex (-4,-2) that is the minimum point of the graph(for y), and it goes up to infinity(really high values). Therefore our range will be [2,∞) and we include the 2 because it is a point on the graph.
That's it! Great Question!