Question

Use g = 10 m/s/s for this problem. A force is applied to a block through tension in a rope, at an angle to the horizontal as shown. The block is being pulled across a rough surface. The mass of the block is 71 kg. The tension in the rope is 1197 N. The angle from horizontal is 15 degrees. The coefficient of friction μ is 0.3.

Answer 1

14.6 m/s²

Step-by-step explanation:

First, we will make the free body diagram

Since the net vertical force is equal to 0 because the block is not moving up, we can write the following equation

`\begin{gathered} F_(nety)=F_n+F_(Ty)-mg=0 \\ F_n+F_T\sin15-mg=0 \end{gathered}`

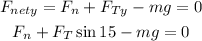
Then, we can solve for the normal force and replace Ft = 1197 N, m = 71 kg and g = 10 m/s²

`\begin{gathered} F_n=mg-F_T\sin15 \\ F_n=(71\text{ kg\rparen\lparen10 m/s}^2)-(1197N)(0.26) \\ F_n=400.2\text{ N} \end{gathered}`

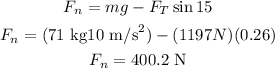
Now, we can write the following equation for the net horizontal force

`\begin{gathered} F_(net)=F_(Tx)-F_f=ma \\ F_T\cos15-\mu F_n=ma \end{gathered}`

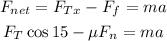
Where μ is the coefficient of friction and a is the acceleration of the block. Solving for a and replacing Ft = 1197 N, m = 71 kg, Fn = 400.2 N and μ = 0.3, we get

`\begin{gathered} a=(F_T\cos15-\mu F_n)/(m) \\ \\ a=\frac{(1197\text{ N\rparen}\cos15-0.3(400.2N)}{71\text{ kg}} \\ \\ a=14.6\text{ m/s}^2 \end{gathered}`

Therefore, the acceleration of the block is 14.6 m/s²