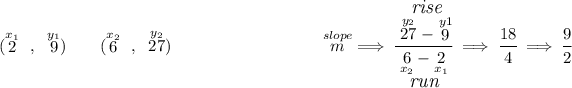the slope goes by several names
• average rate of change
• rate of change
• deltaY over deltaX
• Δy over Δx
• rise over run
• gradient
• constant of proportionality
however, is the same cat wearing different costumes.
to get the slope of any straight line, we simply need two points off of it, let's use those two in the picture below.