Question

You recently bought a new car and arecurious how much it's value drops over timeYou do some research and find out that yourbrand of car depreciates 10% per year andyou bought it new for $12,000. Write anexponential equation to represent the valueof the car, f(x), based on the number of yearssince you bought it (x) (show work)A) how much will your car be worth after5 years?B) how much will your car be worth after12 years?

Answer 1

The price of the car = $12,000

The depreciate by 10%

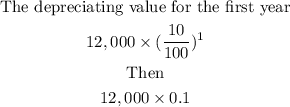
`\begin{gathered} \text{ The depreciating value for the first year } \\ 12,000*((10)/(100))^1 \\ \text{Then} \\ 12,000*0.1 \end{gathered}`

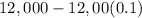
Then

`12,000-12,00(0.1)`

Then

`\begin{gathered} 12000(1-0.1) \\ 12,000(0.9) \end{gathered}`

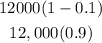
For the first year the depreciating value will be

`12,000(0.9)`

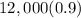
Base on the number of years, the exponential equation will be

`\begin{gathered} f(x)=12,000(0.9)^x \\ \text{where } \\ x=\text{ number of years } \end{gathered}`

Therefore

The exponential equation that represent the value of the car is

F(x)=12,000(0.9)^x

The price of the car in 5 yeras will be obtain by substituting x=5 into the equation above

`\begin{gathered} f(x)=12,000(0.9)^x \\ \text{where x=5} \\ f(x)=12,000(0.9)^5=7085.88 \end{gathered}`

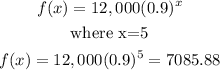
The car will worth $7085.88 after 5 years

Similarly, The for 12 years we have x=12

`f(x)=12,000(0.9)^(12)=3389.15`

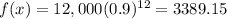
The car will worth $3389.15 after 12 years