The length of BC is 9.33 cm.
In similar triangles, corresponding sides are the sides that are opposite to congruent angles.
From the given information, we know that angle ABC is equal to angle DEF, and angle ACB is equal to angle DFE.
Therefore, the corresponding sides are:
BC corresponds to EF (opposite to equal angles ABC and DEF)
AC corresponds to DF (opposite to equal angles ACB and DFE)
Set up a Proportion:
Since the triangles are similar, the ratios of corresponding sides are equal.
We can set up a proportion using the known side lengths:
AC/DF = BC/EF
Substitute Known Values:
Plug in the given side lengths:
15 cm / 14 cm = DF / 15 cm
Cross-multiply to isolate DF:
15 cm * 14 cm = 15 cm * DF
Simplify:
210 cm² = 15 cm * DF
Divide both sides by 15 cm:
DF = 210 cm² / 15 cm
DF = 14 cm
Now, since the scale factor is mentioned as
 , the length of
, the length of
 (which corresponds to EF) would be:
(which corresponds to EF) would be:

Complete Question:
 and
and
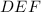 are two similar triangles.
are two similar triangles.
Angle
 Angle
Angle
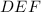
Angle
 Angle
Angle
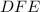
Work out the length o f
 .
.