Question

The current student population of Kansas City is 2700. If the population increases at a rate of 5.2% each year. What will the student population be in 4 years?Write an exponential growth model for the future population P(x) where x is in years:p(x)=What will the population be in 4 years? (Round to nearest student)

Answer 1

P(x) = 2700(1.052)^t

P(4) = 3307. (Rounded to nearest student)

Step-by-step explanation

Given:

1. The current student population to be 2700

2. The growth rate = 5.2% = 0.052

Desired Outcome

1. The exponential growth model

2. Population of the students in 4 years

The Exponential Growth Model

`\begin{gathered} P(x)\text{ = 2700\lparen1 + 0.052\rparen}^t \\ P(x)\text{ = 2700\lparen1.052\rparen}^t \end{gathered}`

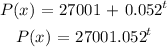
Population in 4 years

`\begin{gathered} P(4)\text{ = 2700\lparen1.052\rparen}^4 \\ P(4)\text{ = 2700}*1.2248 \\ P(4)\text{ = 3306.96} \end{gathered}`

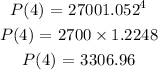
Hence, the Exponential Growth Model P(x) = 2700(1.052)^t and the Population of the students in 4 years P(4) = 3307. (Rounded to nearest student)