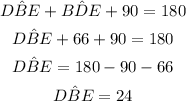(i)
The angle 78° is supplementary to the angle BCE. Then we have:
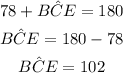
(ii)
When the vertex of a angle formed by two segments is located on the circle, the corresponding arc formed by the two segments is the double of the angle. Then we have:
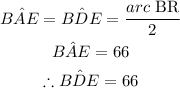
(iii)
Since BDE is a right triangle, we have: