Question

The diagram shows a rectangle. The width of the rectangle is 8 cm. The length of the rectangle is 3y + 4 cm. Write an expression, in its simplest form, for the: (Don't write cm) a perimeter of the rectangle b area of the rectangle

Answer 1

a. 6y+12

b. 24y+28

Explanation:

a.

The perimeter of a rectangle can be found using the formula
`P = 2(l+w)`.
`P` is the perimeter,
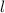`l` is the length, and
`w` is the width.
The diagram (?) shows a rectangle, which is disclosed (in the future, you won't always know whether a shape is a rectangle or not, the problem needs to let you know). The width is given as 8 cm, and the length is given as
`3y + 4` cm.

Using the formula and the information above, we can conclude that the area of the rectangle is
`2*(8+3y+4) = 2*(12+3y)`.

We distribute the 2 among the expression
`3y+12` to get
`6y+24`.

b.

The area of a rectangle can be found by multiplying the length of the rectangle (
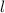`l`) by the width of the rectangle (
`w`), or by using the formula
`A = l*w`, where
`A` is the area.
Using the information given (
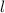`l` = 3y+4, and
`w` = 8), we can multiply the two values together.

`A = l*w\\A = (3y+4)*(8)\\A = 8(3y+4)\\A = 24y+28`

(Please let me know if I made any mistakes.)