Question

Graph the solution of inequalities and shade in the solution set. If there are no solutions, graph the corresponding line and do not shade in any region. Y = grater and equal to 1/2x - 3 Y < - 2/3 x + 2

Answer 1

`\begin{gathered} y\ge(1)/(2)x-3 \\ y<-(2)/(3)x+2 \end{gathered}`

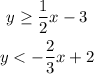
start sketching the first inequality taking into account that it is all the region above the line of slope 1/2 and crosses over -3

then, do the same for the second equation over the same plane and look at the intersection

the shaded region should be the triangle at the left since the region is a solution to both inequalities.