Question

Use the function f(x)=x 2 −6x+8 to answer the following questions: a. What is the y-intercept? b. What are the x-intercepts? c. What is the vertex? d. What is the axis of symmetry?

Answer 1

see explanation

Explanation:

given the function

f(x) = x² - 6x + 8

(a)

to find the y- intercept , let x = 0 in f(x)

f(0) = 0² - 6(0) + 8 = 0 - 0 + 8 = 8 ← y- intercept

(b)

to find the x- intercepts , let f(x) = 0 , that is

x² - 6x + 8 = 0 ← in standard form

(x - 2)(x - 4) = 0 ← in factored form

equate each factor to zero and solve for x

x - 2 = 0 ⇒ x = 2

x - 4 = 0 ⇒ x = 4

the x- intercepts are x = 2 and x = 4 or (0, 2 ), (0, 4 ) in coordinate form

(c)

given a quadratic in standard form

f(x) = ax² + bx + c ( a ≠ 0 )

then the x- coordinate of the vertex is

`x_(vertex)` = -
`(b)/(2a)`

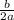
f(x) = x² - 6x + 8 ← is in standard form

with a = 1 and b = - 6 , then

`x_(vertex)` = -
`(-6)/(2)` = - (- 3) = 3

evaluate f(3) for corresponding y- coordinate

f(3) = 3² - 6(3) + 8 = 9 - 18 + 8 = - 9 + 8 = - 1

vertex = (3, - 1 )

(d)

the axis of symmetry is a vertical line , passing through the vertex with equation

x = c ( c is the value of the x- coordinate of the vertex )

equation of axis of symmetry is then x = 3