Question

A rock is thrown upward from the top of a 80-foot high cliff overlooking the ocean at a speed of 64 feetper second The rock's height above ocean can be modeled by the equationH (t) = -16t^2 +64t + 80.a. When does the rock reach the maximum height?The rock reaches its maximum height after ________second(s).b. What is the maximum height of the rock?The maximum height obtained by the rock is_______feet above sea level.c. When does the rock hit the ocean?The rock hits the ocean after_____seconds.

Answer 1

Given:

The speed is 64 feet per second.

The height of the high cliff is 80 feet.

The function is

`H(t)=-16t^2+64t+80`

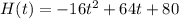
a)

We need to find the maximum value of t in the given function to find a time when the rock reaches its maximum height.

Differentiate the given equation, we get

`H^(\prime)(t)=-16(2t)^{}+64`

`H^(\prime)(t)=-32t^{}+64`

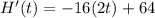
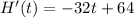
Set H'(t)=0 and solve for t.

`0=-32t^{}+64`

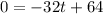
Adding 32t on both sides, we get

`0+32t^{}=-32t+64+32t`

`32t^{}=64`

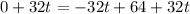
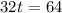
Dividing both sides by 32, we get

`(32t)/(32)^{}=(64)/(32)`
`t=2`

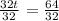
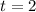
Hence the rock reaches its maximum height after 2 seconds.

b)

Substitute t=2 in the given equation to find the maximum height of the rock.

`H(2)=-16(2)^2+64(2)+80`

`H(2)=144`

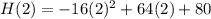
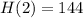
Hence the maximum height obtained by the rock is 144 feet above sea level.

c)

Substitute H(t)=0 in the given function to find the time when the rock hit the ocean.

`0=-16t^2+64t+80`

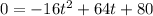
Dividing both sides by (-16), we get

`0=-(16t^2)/(-16)+(64t)/(-16)+(80)/(-16)`
`0=t^2-4t-5`

`t^2-4t-5=0`

`t^2+t-5t-5=0`

`t(t+1)-5(t+1)=0`

`(t+1)(t-5)=0`

`(t+1)=0,(t-5)=0`
`t=-1,t=5`

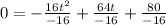
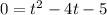
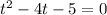
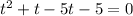
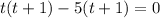
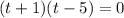
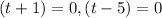
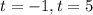
Omitting the negative value, we get t= 5 seconds.

Hence the rock hits the ocean after 5 seconds.