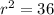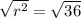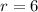Answer: Center: (2, –4); Radius: 6.
Step-by-step explanation
The equation of a circle in standard form is:

where (h, k) is the center and r is the radius. Thus, in our given equation:
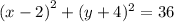
• h = 2
,
• k = –4 (it is negative as negative sign times negative sign equals positive sign)
,
• r² = 36
Therefore, the center is (2, –4) and the radius is: