Question

Grandma lives 120 miles away. Dinner is at 5 p.m. The speed limit is 60 mph. What time do you need to leave to be on time?

Answer 1

Given data:

* The distance to the Grandma house is d = 120 miles.

* The value of the speed limit is v = 60 mph.

* The time for the dinner is t = 5 p.m.

Solution:

The time taken to reach the Grandma house while moving in the speed limit is,

`\begin{gathered} v=(d)/(T) \\ T=(d)/(v) \end{gathered}`

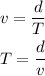
Substituting the known values,

`\begin{gathered} T=(120)/(60) \\ T=2\text{ hours} \end{gathered}`

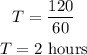
The time of leaving is,

`\begin{gathered} t_1=t-T \\ t_1=5-2 \\ t_1=3\text{ p.m.} \end{gathered}`

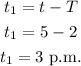
Thus, the time at which the person should leave for grandma's house is 3 p.m.