Question

The exact Value of the sine, cosine, and tangent about of the angle

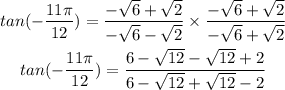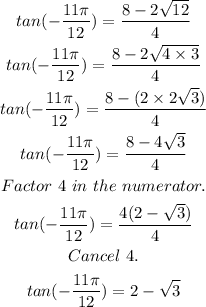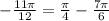
Answer 1

`-(11\pi)/(12)=(\pi)/(4)-(7\pi)/(6)`

Below are the exact values of sine, cosine, and tangent of the given angle -11π/12.

`sin(-(11\pi)/(12))=(-√(6)+√(2))/(4)`
`cos(-(11\pi)/(12))=(-√(6)-√(2))/(4)`
`tan(-(11\pi)/(12))=(sin(-(11\pi)/(12)))/(cos(-(11\pi)/(12)))=2-√(3)`

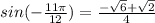
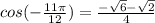
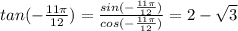
Step-by-step explanation:

We can use the following trigonometric identities to solve the exact value of the given angle.

`\begin{gathered} sin(x+y)=sin\text{ }x\text{ }cos\text{ }y+cos\text{ }x\text{ }sin\text{ }y \\ cos(x+y)=cos\text{ }x\text{ }cos\text{ }y-sin\text{ }x\text{ }sin\text{ }y \end{gathered}`

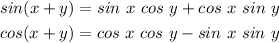
For sine function, we have:

`\begin{gathered} sin(-(11\pi)/(12))=sin((\pi)/(4)-(7\pi)/(6)) \\ sin((\pi)/(4)-(7\pi)/(6))=sin\text{ }(\pi)/(4)cos(-(7\pi)/(6))+cos\text{ }(\pi)/(4)sin(-(7\pi)/(6)) \end{gathered}`

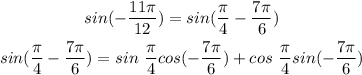
Simplify.

`\begin{gathered} sin((\pi)/(4)-(7\pi)/(6))=(√(2))/(2)(-(√(3))/(2))+(√(2))/(2)((1)/(2)) \\ sin((\pi)/(4)-(7\pi)/(6))=(-√(6))/(4)+(√(2))/(4) \\ sin((\pi)/(4)-(7\pi)/(6))=(-√(6)+√(2))/(4) \\ sin(-(11\pi)/(12))=(-√(6)+√(2))/(4) \end{gathered}`

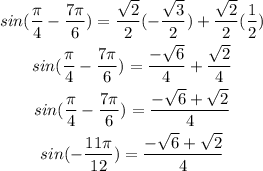
For cosine function, we have:

`\begin{gathered} cos(-(11\pi)/(12))=cos((\pi)/(4)-(7\pi)/(6)) \\ cos((\pi)/(4)-(7\pi)/(6))=cos(\pi)/(4)cos(-(7\pi)/(6))-sin(\pi)/(4)sin(-(7\pi)/(6)) \end{gathered}`

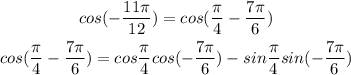
Simplify.

`\begin{gathered} cos((\pi)/(4)-(7\pi)/(6))=(√(2))/(2)(-(√(3))/(2))-((√(2))/(2))((1)/(2)) \\ cos((\pi)/(4)-(7\pi)/(6))=(-√(6))/(4)-(√(2))/(4) \\ cos((\pi)/(4)-(7\pi)/(6))=(-√(6)-√(2))/(4) \\ cos(-(11\pi)/(12))=(-√(6)-√(2))/(4) \end{gathered}`

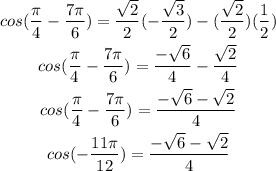
Lastly, for tangent function, it is the ratio between sine and cosine function.

`tan(-(11\pi)/(12))=(sin(-(11\pi)/(12)))/(cos(-(11\pi)/(12)))`

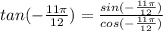
Applying the division rule, we get the reciprocal of the denominator and multiply it to the numerator. The equation becomes:

`tan(-(11\pi)/(12))=sin(-(11\pi)/(12))*(1)/(cos(-(11\pi)/(12)))`

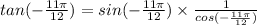
Now, let's replace the sine and cosine value that we have calculated above.

`tan(-(11\pi)/(12))=(-√(6)+√(2))/(4)*(4)/(-√(6)-√(2))`

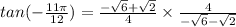
Since 4 is a common factor on both numerator and denominator, we can cancel it out. The equation then becomes,

`tan(-(11\pi)/(12))=(-√(6)+√(2))/(-√(6)-√(2))`

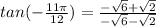
To further simplify the function, let's remove the radicals in the denominator by rationalization.

`\begin{gathered} tan(-(11\pi)/(12))=(-√(6)+√(2))/(-√(6)-√(2))*(-√(6)+√(2))/(-√(6)+√(2)) \\ tan(-(11\pi)/(12))=(6-√(12)-√(12)+2)/(6-√(12)+√(12)-2) \end{gathered}`
`\begin{gathered} tan(-(11\pi)/(12))=(8-2√(12))/(4) \\ tan(-(11\pi)/(12))=(8-2√(4*3))/(4) \\ tan(-(11\pi)/(12))=(8-(2*2√(3)))/(4) \\ tan(-(11\pi)/(12))=(8-4√(3))/(4) \\ Factor\text{ }4\text{ }in\text{ }the\text{ }numerator. \\ tan(-(11\pi)/(12))=(4(2-√(3)))/(4) \\ Cancel\text{ }4. \\ tan(-(11\pi)/(12))=2-√(3) \end{gathered}`