Question

What is the approximate area of sector ABC with central angle Θ≈56°? Round your answer to the nearest hundredth.

Question 3 options:

72.56 cm²


80.29 cm²


60.66 cm²


70.34 cm²

Answer 1

70.34 cm²

Explanation:

The area of a sector is the ratio between the sector's central angle θ and 360 degrees times the area of the whole circle.

The area of a sector is given by the following formula:

`\sf \textsf{Area of sector} =(\theta)/(360^\circ) \pi r^2`

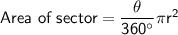
where:

• θ is the central angle of the sector in degrees
• π is a mathematical constant with the approximate value of 3.14
• r is the radius of the circle

In this case:

We have

• θ = 56°
• r = 12 cm
• π = 3.14

Substituting value in above formula, we get

`\sf \textsf{Area of sector} =(56^\circ )/(360^\circ) \cdot 3.14 \cdot 12^2`

`\sf \textsf{Area of sector} =(56^\circ )/(360^\circ) \cdot 3.14 \cdot 144 cm^2`

`\sf \textsf{Area of sector} =(56^\circ )/(360^\circ) \cdot 452.16 cm^2`

`\sf \textsf{Area of sector} = 70.34 cm^2 \textsf{ in nearest hundred}`

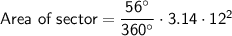
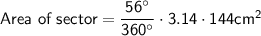
Therefore, the area of the sector is 70.34 cm²