Question

Write an equation is slow intercept form of the line that passes through the given points and its parallel to the graph of the given equation.

(-8,-3) y= -2x+5
write an equation for the line and slope intercept form
please help I’ve been up all night

Answer 1

y = - 2x - 19

Explanation:

In order to find the equation of the line parallel to y =- 2x + 5 that passes through the point (-8,-3), we can use the following steps:

Finding the slope of the parallel line.

Comparing the above equation with y = mx + c, we get slope(m) = -2.

Since parallel lines have the same slope, the slope of the parallel line is also -2.

Using the point-slope form to find the equation of the parallel line.

The point-slope form of the equation of a line is:

`\sf y - y_1 = m(x - x_1)`

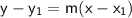
where m is the slope of the line and
`\sf (x_1, y_2)` is a point on the line.

Substituting the slope and point (-8,-3) into the point-slope form, we get the following equation:

y - (-3) = -2(x - (-8))

y + 3 = -2(x + 8)

Open the bracket by distributing -2.

y + 3 = -2x - 16

Subtract 3 on both sides.

y + 3 - 3 = -2x - 16 - 3

y = -2x - 19

Therefore, the equation of the line parallel to y=-2x+5 that passes through the point (-8,-3) in slope intercept form is y=-2x-19.

Answer 2

y = -2x - 19

Explanation:

The slope-intercept form of a linear equation is:

`\large\boxed{y = mx + b}`

where:

• m is the slope.
• b is the y-intercept.

To find the equation of a line that passes through the point (-8, -3) and is parallel to the graph of the equation y = -2x + 5, we can use the fact that parallel lines have the same slope.

The given equation has a slope of m = -2. So, the equation of the parallel line also has a slope of m = -2.

Substitute the slope m = -2 and the point (-8, 3) into the slope-intercept formula to find the y-intercept (b) of the parallel line:

`-3 = -2(-8) + b`

`-3 = 16 + b`

`-19=b`

`b=-19`

Therefore, the y-intercept of the parallel line is b = -19.

Substitute the slope (m = -2) and the y-intercept (b = -19) into the slope-intercept formula to write the equation of the line that passes through the point (-8, -3) and is parallel to the graph of the equation y = -2x + 5:

`\Large\boxed{\boxed{y = -2x - 19}}`