Question

Find the length of side x to the nearest tenth.

Answer 1

Given:-

• A right angled triangle is given to us .
• Two angles are 60° and 30° , longest side is x and another side is "2" .

To find:-

• The value of x .

Answer:-

In the given right angled triangle, we may use the trigonometric ratios. We can see that the measure of the longest side is "x" which is hypotenuse and it needs to be find out. The perpendicular in this case is "2" .

We may use the ratio of sine here as , we know that in any right angled triangle,

`\implies\sin\theta =(p)/(h) \\`

And here , p = 2 and h = x , so on substituting the respective values, we have;

`\implies \sin\theta = (2)/(x) \\`

Again here angle is 60° . So , we have;

`\implies \sin60^o =(2)/(x) \\`

The measure of sin45° is √3/2 , so on substituting this we have;

`\implies (\sqrt3)/(2)=(2)/(x) \\`

`\implies x =(2\cdot 2)/(\sqrt3)\\`

Value of √3 is approximately 1.732 . So we have;

`\implies x =(4)/(1.732) \\`

`\implies \underline{\underline{\red{\quad x = 2.31\quad }}}\\`

Hence the value of x is 2.31 .

Answer 2

The length of side x to the nearest tenth is 2.3.

Explanation:

From inspection of the given right triangle, we can see that the interior angles are 30°, 60° and 90°. Therefore, this triangle is a 30-60-90 triangle.

A 30-60-90 triangle is a special right triangle where the measures of its sides are in the ratio 1 : √3 : 2. Therefore, the formula for the ratio of the sides is b: b√3 : 2b where:

• b is the shortest side opposite the 30° angle.
• b√3 is the side opposite the 60° angle.
• 2b is the longest side (hypotenuse) opposite the right angle.

We have been given the side opposite the 60° angle, so:

`\implies b√(3)=2`

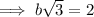
Solve for b by dividing both sides of the equation by √3:

`\implies b=(2)/(√(3))`

The side labelled "x" is the hypotenuse, so:

`\implies x=2b`

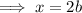
Substitute the found value of b into the equation for x:

`\implies x=2 \cdot (2)/(√(3))`

`\implies x=(4)/(√(3))`

`\implies x=2.30940107...`

`\implies x=2.3\; \sf (nearest\;tenth)`

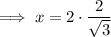
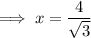
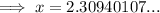
Therefore, the length of side x to the nearest tenth is 2.3.