Question

For the literal equation x^2+m=y, express x in terms of y and m

Answer 1

We have the equation of y as a function of x:

`y(x)=x^2+m`

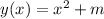
To find x(y) we just need to solve for x, first by subtracting m from both sides

`y-m=x^2`

Now, we just have to take the square root on both sides

Taking the square root of a number it's actually raising it to the 1/2 power:

`\sqrt[]{a}=a^{(1)/(2)}`

Now, when we proceed to raise the square root of a number to two, we can arrange it like this:

`(a^{(1)/(2)})^2=a^{(2)/(2)}=a^1=a`

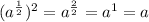
When we take the square root of a number that is raised to two the result will be the number without any power, like this:

`\sqrt[]{a^2}=a`

Then:

`\sqrt[]{x^2}=x=\sqrt[]{y-m}`