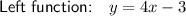Question

50 Points
Dont Troll

Answer 1

i believe p = 1/4 and q = 4

lmk if that was right!

Answer 2

`\textsf{C.\quad$p=(1)/(4)$\;\;and\;\;$q=4$}`

Explanation:

The slope of a line shows the direction and steepness of the line.

It is the ratio of the rise to the run (the change in y divided by the change in x).

The slope of the left function is 4, as we can see that when the y-value increases by 4 units (the "rise"), the x-value increases by 1 unit (the "run").

The slope of the right function is 1, as we can see that when the y-value increases by 1 unit (the "rise"), the x-value increases by 1 unit (the "run").

Given the slope of the function on the left is multiplied by p to arrive at the slope of the function on the right:

`\implies 4p=1`

`\implies (4p)/(4)=(1)/(4)`

`\implies p=(1)/(4)`

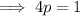
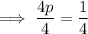
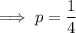
The y-intercept is the point at which the line crosses the y-axis.

The left function crosses the y-axis at (0, -3), so its y-intercept is y = -3.

The right function crosses the y-axis at (0, 1), so its y-intercept is y = 1.

Given q is added to the y-intercept of the function on the left to arrive at the y-intercept of the function on the right:

`\implies -3+q=1`

`\implies -3+q+3=1+3`

`\implies q=4`

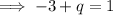
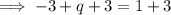
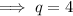
Solution

`\textsf{$p=(1)/(4)$\;\;and\;\;$q=4$}`

The equations of the functions are:

`\textsf{Left\;function:\quad $y=4x-3$}`

`\textsf{Right\;function:\quad $y=x+1$}`