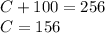Question

the admission fee at an amusement park is $1.50 for children and $6.20 for adults. On a certain day, 256 people entered the park, and the admission fees collected totaled $854. How many children and how many adults were admitted?

Answer 1

C = 156 children

A = 100 adults

Explanation:

We will need a system of equations to find the number of children and adults admitted to the amusement park.

Because the number of children + the number of adults = the total number of people admitted (256), one of our equations is C + A = 256, where C is the total number of children admitted and A is the total number of adults admitted.

Because the revenue earned from the children ($1.50/child) + the revenue earned from the adults ($6.20/adult) = the total revenue earned ($854), our other equation is 1.50C + 6.20A = 854

It will be easier to isolate C in the first equation and then substitute it into the second equation:

`C+A=256\\C=-A+256\\\\1.50(-A+256)+6.20A=854\\-1.50A+384+6.20A=854\\4.70A+384=854\\4.70A=470\\A=100`

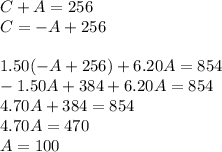
Now, we can substitute this 100 for A in the first equation to find the total number of children admitted:

`C+100=256\\C=156`