The Solution:
Step 1:
We shall state the formula for calculating Z-score.
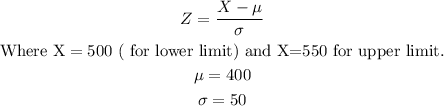
Step 2:
We shall substitute the above values in the formula.
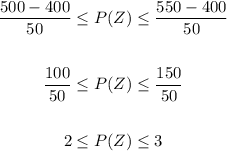
Step 3:
We shall read the respective probabilities from the Z score distribution tables.
From the Z-score tables,
P(3) = 99.9 %
P(2) = 97.7 %
Step 4:
The Conclusion:
The probability that a worker selected makes between $500 and $550 is obtained as below:
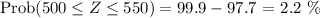
Therefore, the required probability is 2.2 %