Answer:
Common ratio = 1.75
17th term = 123,802.31
Explanations:
Given the following parameters:
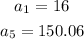
Since the sequence is geometric, the nth term of the sequence is given as;
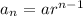
a is the first term
r is the common ratio
n is the number of terms
If the first term a1 = 16, then;
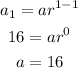
Similarly, if the fifth term a5 = 150.06, then;

Hence the common ratio to the nearest hundredth is 1.75
Next is to get the 17th term as shown;
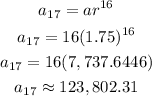
Hence the 17th term of the sequence to the nearest hundredth is 123,802.31