Given,
The coordinate that lie on the line is (-4, -3).
The equation of line is y = 3/4x-1.
The standard equation of line is,
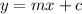
Here, m is the slope of the line.
On comparing, the slope of the line y = 3/4x-1 with the standard equation of line then m = 3/4.
The relation of two perpendicular line is,
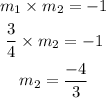
The equation of line passing through the point (-4,-3) and perpendicular to line y = 3/4x-1 is,

Hence, the equation of line perpendicular to y = 3/4x-1 is y = (-4x-25)/3.