SOLUTION
The limit of a function at a point aa in its domain (if it exists) is the value that the function approaches as its argument approaches a.
The limit of a function F exist if and only if
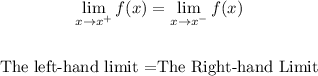
Considering the image given, the limit of the function from the left is from the first graph
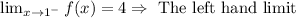
Similarly, the limit of f(x) from the right-hand side is on the second graph
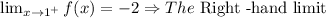
Since
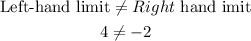
Therefore
The Limit does not exist (D)