Question

Consider a circle whose equation is x2 + y2 – 2x – 8 = 0. Which statements are true? Select three options. The radius of the circle is 3 units. The center of the circle lies on the x-axis. The center of the circle lies on the y-axis. The standard form of the equation is (x – 1)² + y² = 3. The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

Answer 1

The true statements are:

• The radius of the circle is 3 units.
• The center of the circle lies on the x-axis.
• The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

Explanation:

The general equation of a circle is:

`\boxed{(x - h)^2 + (y - k)^2 = r^2}`

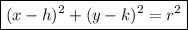
where:

• (h, k) is the center of the circle.
• r is the radius of the circle.

To rewrite the given equation x² + y² - 2x - 8 = 0 in standard form, begin by moving the constant to the right side of the equation and collect like terms on the left side of the equation:

`\implies x^2-2x+y^2=8`

Add the square of half the coefficient of the term in x to both sides of the equation. (As there is no term in y, we do not need to add the square of half the coefficient of the term in y):

`\implies x^2-2x+\left((-2)/(2)\right)^2+y^2=8+\left((-2)/(2)\right)^2`

Simplify:

`\implies x^2-2x+1+y^2=9`

Factor the perfect square trinomial in x:

`\implies (x-1)^2+y^2=9`

We have now written the equation in standard form.

Comparing this with the standard form equation, we can say that:

• 
  `h = 1`
• 
  `k = 0`
• 
  `r^2 = 9 \implies r = √(9) = 3`

Therefore, the center of the circle (h, k) is (1, 0) and its radius is 3 units.

As the y-coordinate of the center is zero, the center lies on the x-axis.

Therefore, the true statements are:

• The radius of the circle is 3 units.
• The center of the circle lies on the x-axis.
• The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.