Question

Suppose tan(b) = –2, and the terminal side of b is located in quadrant II. What is cot(b)

a. ) –2

b. ) Negative one-half

c. ) one-half

d. )2

Answer 1

b) Negative one-half

Explanation:

according to the equation:

`\tan(b)=-2\\\therefore b=\tan^1(-2})\\b=-63.44^\circ`

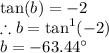
This value is located in the IV quadrant, however we can add 180 degrees and still remain the same value

`b \equiv -63.44+180\\b \equiv 116.56^\circ`

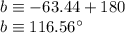
Now, "b" is located in the II quadrant, so:

`cot(116.56)= ?`

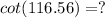
I guess you want to get the result with calculator, so we will use an identity to be able to enter this value into the calculator.

`cot(116.56)= (1)/(tan(116.56)) \approx -0.5`

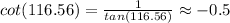
Therefore, we have found the solution to the exercise.

`\text{-B$\mathfrak{randon}$VN}`