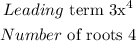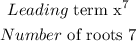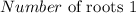Question

ANSWER IMMEDIATELY PLEASE Identify the number of roots each polynomial has.Number one. 3x^4-2x^2+17x-4Number two. 12x^5+x^7-8+4x^2Number 3. 15+6x

Answer 1

Step 1

The degree of the leading term determines how many roots a polynomial has. Examine the highest-degree term of the polynomial – that is, the term with the highest exponent. That exponent is how many roots the polynomial will have. So if the highest exponent in your polynomial is 2, it'll have two roots; if the highest exponent is 3, it'll have three roots; and so on. A polynomial with a leading degree of 5 has 5 roots.

Step 2

`\begin{gathered} Leading\text{ term 3x}^4 \\ Number\text{ of roots 4} \end{gathered}`

`\begin{gathered} Leading\text{ term x}^7 \\ Number\text{ of roots 7} \end{gathered}`

`Number\text{ of roots 1}`