Hello there. To solve this question, we'll have to remember some properties about rectangles.
A rectangle is a quadrilateral polygon (that is, it has 4 right angles in its corners) and two parallel sides.
The special cases of quadrilaterals are the parallelogram, that has two parallel sides but the angles might not be right angles and the square, in which the sides are equal.
In the case of the rectangle, it has a side with length L and other side, that we call its width, with length W, as in the following drawing:
Its area A can be calculated taking the product between the length and the width, therefore:

With this, we can solve this question.
It says that a rectangle is 15 ft longer than it is wide. Its area is 2700 ft². We have to determine its dimensions.
Say this rectangle has width W.
If this rectangle is 15 ft longer than it is wide, it means that
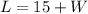
Now, we plug this values for the formula of area, knowing that A = 2700:

Apply the FOIL
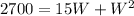
In this case, we have a quadratic equation in W.
We'll solve it by completing the square, that is, finding a perfect trinomial square such that we can undo the binomial expansion and solve a simpler quadratic equation.
The binomial expansion (a + b)² gives us
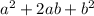
So to find the b we need to complete the square, we start dividing the middle term by 2.
In the case of our equation, the middle term has coefficient 15, hence

Square the number and add it on both sides of the equation, such that
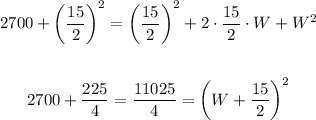
Take the square root on both sides of the equation, knowing that 11025 = 105²
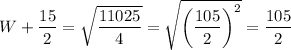
Subtract 15/2 on both sides of the equation
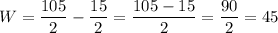
Then we plug this value in the expression for L, hence we get:
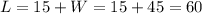
Notice that multiplying the numbers, we'll get:
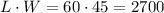
That is exactly the area we had before.
Hence we say that its width equals 45 ft and its length equals 60 ft.