Question

Solve for the remaining angles and side of the two triangles that can be created. Round to the nearest hundredth:B = 30 .b = 6,a = 7AnswerHow to enter your answer (opens in new window) 2 PointsTriangle 1: (where angle A is acute):Triangle 2: (where angle A is obtuse):AA:C =C:C:

Answer 1

Triangle 1:

A = 35.69°

C = 114.31°

c = 10.94

Triangle 2:

A = 144.31°

C = 5.69°

c = 1.19

Explanation:

Given:

B = 30°, b = 6, a = 7

We calculate the angle A by means of the law of sines:

`\begin{gathered} (a)/(\sin A)=(b)/(\sin B) \\ \\ \text{ We replacing} \\ \\ (7)/(\sin A)=(6)/(\sin30) \\ \\ \sin A=(7)/(6)\cdot\sin30 \\ \\ \sin A=(7)/(12) \\ \\ A=\sin^(-1)\left((7)/(12)\right)\: \\ \\ A_(acute)=35.69\degree \\ \\ A_(obtuse)=144.31\degree \end{gathered}`

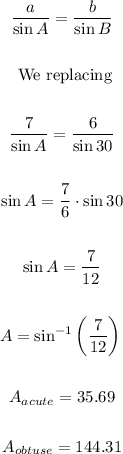
We calculate the value of angle C, knowing that the sum of all internal angles is equal to 180°

`\begin{gathered} \text{ Acute} \\ \\ 180=35.69+30+C \\ \\ C=180-30-35.69=114.31\degree \\ \\ \text{ Obtuse} \\ \\ 180=144.31+30+C \\ \\ C=180-30-144.31=5.69\degree \end{gathered}`

Side c is also calculated with the law of sines, like this:

`\begin{gathered} \text{ Acute} \\ \\ (b)/(\sin B)=(c)/(\sin C) \\ \\ (6)/(\sin(30))=(c)/(\sin114.31) \\ \\ c=(6)/(\sin(30))\cdot\sin114.31 \\ \\ c=\:10.94 \\ \\ \text{ Obtuse} \\ \\ (7)/(\sin(A))=(c)/(\sin(C)) \\ \\ c=(6)/(\sin(30))\sin(5.69) \\ \\ c=1.19 \end{gathered}`

Therefore;

Triangle 1:

A = 35.69°

C = 114.31°

c = 10.94

Triangle 2:

A = 144.31°

C = 5.69°

c = 1.19