Question

I take my calculator from the top of a building and toss it straight upward at 9 m/s from a 23 m tall building.A. what is the speed of the Calculator right before it hits the ground? B. What is the acceleration of the calculator at peak height? C. How much time does it take for the calculator to reach peak height?

Answer 1

Given,

The initial velocity with which the calculator was thrown, u=9 m/s

The height of the building, h=23 m

A.

When the calculator reaches the peak height, its velocity will become zero. That is v=0 m/s

And while it is going up the acceleration due to gravity will be acting downward. Thus the acceleration due to gravity will be a negative value.

From the equation of motion,

`v^2-u^2=2gs_{}`

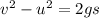
Where s is the peak height reached by the calculator and g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} 0-9^2=2*-9.8* s \\ \Rightarrow s=(-9^2)/(2*-9.8) \\ =4.13\text{ m} \end{gathered}`

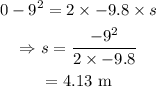
Thus the total height reached by the calculator from the ground is

`\begin{gathered} H=h+s \\ =23+4.13 \\ =27.13 \end{gathered}`

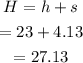
After reaching the peak height, the calculator starts descending. This descent starts with the initial velocity of v=0 m/s. And the acceleration due to gravity will be in the direction of motion of the calculator. Thus it will be a positive value.

From the equation of motion,

`v^2_0-v^2=2gH`

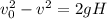
where v₀ is the velocity of the calculator right before it hits the ground.

On substituting the known values,

`\begin{gathered} v^2_0-0=2*9.8*27.13 \\ \Rightarrow v_0=\sqrt[]{2*9.8*27.13}^{} \\ =23.06\text{ m/s} \end{gathered}`

Thus the speed of the calculator right before it hits the ground is 23.06 m/s

B.

The acceleration of the calculator is a constant value. It is always equal to the acceleration due to gravity.

Thus the acceleration of the calculator at peak height is 9.8 m/s²

C.

From the equation of motion,

`v=u+gt`

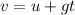
Where t is the time it takes for the calculator to reach the peak height.

On substituting the known values,

`\begin{gathered} 0=9+(-9.8)t \\ \Rightarrow t=(-9)/(-9.8) \\ =0.92\text{ s} \end{gathered}`

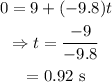
Thus it takes 0.92 s for the calculator to reach the peak height.