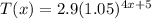Question

answer.The number of cities in a region over time is represented by the function C(=) = 2.9(1.05). The approximate number of people per city isrepresented by the function P(t) = (1.05)35 +5.Which function best describes T(*), the approximate population in the region?OA T(I) = (3.045)* + (1.05)35 +5OB. T(1) = (6.09)45+5OC. T() = 2.9(1.05)45+5OD. Т(1) = 2.9(1.05)352 +55

Answer 1

Given:

`\begin{gathered} \text{Number of cities: }C(x)=2.9(1.05)^x \\ \\ \text{Number of people per city: P}(x)=(1.05)^(3x+5) \end{gathered}`

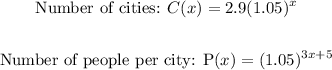
Let's solve for T(x) which represents the approximate population in the region.

To find the approximate population in the region, apply the formula:

`T(x)=C(x)\ast P(x)`

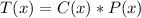
Thus, we have:

`T(x)=2.9(1.05)^x\ast(1.05)^(3x+5)^{}`

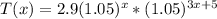
Let's solve the equation for T(x).

Thus, we have:

`\begin{gathered} T(x)=2.9((1.05)^(3x+5)(1.05)^x) \\ \\ Apply\text{ power rule:} \\ T(x)=2.9(1.05)^{3x+5+x^{}_{}} \\ \\ T(x)=2.9(1.05)^(3x+x+5) \\ \\ T(x)=2.9(1.05)^(4x+5) \end{gathered}`

Therefore, the function that best describes the approximate population in the region is:

`T(x)=2.9(1.05)^(4x+5)`

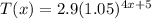
ANSWER:

C

`T(x)=2.9(1.05)^(4x+5)`