Question

spherical balloon is inflated with gas at the rate of 800 cubic centimeters per minute.Find the rates of change of the radius when r=30 centimeters and r=85 centimeters.Explain why the rate of change of the radius of the sphere is not constant even though dV/dt is constant.

Answer 1

Step-by-step explanation

Given:

A spherical balloon is inflated with gas at the rate of 800 cubic centimeters per minute means

`(dV)/(dt)=800\text{ }cm^3\text{/}min`

(a) The rates of change of the radius when r = 30 centimeters and r = 85 centimeters is calculated as follows:

`\begin{gathered} V=(4)/(3)\pi r^3 \\ \\ (dV)/(dr)=(4)/(3)*3\pi r^(3-1) \\ \\ (dV)/(dr)=4\pi r^2 \\ \\ But\frac{\text{ }dV}{dr}=(dV)/(dt)/(dr)/(dt) \end{gathered}`

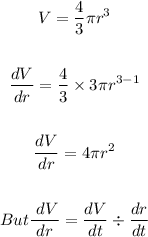
So when r = 30, we have

`\begin{gathered} (dV)/(dr)=4\pi(30)^2 \\ \\ (dV)/(dr)=4*\pi*900 \\ \\ (dV)/(dr)=3600\pi \\ \\ From\text{ }(dV)/(dr)=(dV)/(dt)/(dr)/(dt) \\ \\ Putting\text{ }(dV)/(dt)=800,\text{ }we\text{ }have \\ \\ 3600\pi=800/(dr)/(dt) \\ \\ (dr)/(dt)=(800)/(3600\pi)=(800)/(3600*3.14) \\ \\ (dr)/(dt)=0.071\text{ }cm\text{/}min \end{gathered}`

Therefore, the rate of change of the radius when r = 30 is dr/dt = 0.071 cm/min.

For when r = 25 cm, the rate of change is: