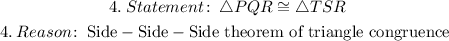Question

I keep overthinking and confusing myself can you help me please

Answer 1

We are asked to prove that triangles △PQR and △TSR are congruent.

Let us write the statements and reasons to prove that the given triangles are congruent.

`\begin{gathered} 1.\: Statement\colon\: \bar{PQ}\cong\bar{TS} \\ 1.Reason\colon Given \end{gathered}`

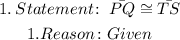
We are given that R is the midpoint of QS and PT

This means that QR ≅ SR and also PR ≅ TR by the property of "Definition of midpoint"

So, now we have 3 equal sides in both triangles

Therefore, by the property of "Side-Side-Side" (SSS) the given triangles are congruent.

`\begin{gathered} 4.\: Statement\colon\: \triangle PQR\cong\triangle TSR \\ 4.\: Reason\colon\: \text{Side}-\text{Side}-\text{Side theorem of triangle congruence } \end{gathered}`