Recall that the centroid of the triangle is the intersection point of its medians, which are the lines that are formed by joining the midpoint of one side with the remainding vertex of the triangle. This point has the property that for each median it splits it in two smaller segments, one of which has the double of the length of the other.
We are given the following picture
Let us call the lenght of GF x. Since G is the centroid, then the length of BG is 2x. Note that the sum of the length of BG plus the length of GF should be BF. So we have the following equation
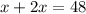
Now, we should solve this equation for x. First we add the x terms on the left. So we get
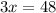
Finally, we divide by 3 on both sides, so we get

so the lenght of GF is 16. Now, si BG has the double length of FG, then the length of BG is 16*2 = 32.