Question

A 7m long ladder leans against a wall such that the foot of the ladder is 4.5m away from the wall. What is the angle of elevation of the ladder?

Answer 1

Given:

• Height of ladder = 7 m

,

• DIstance of foot of ladder to the wall = 4.5 m

Let's find the angle of elevation of the ladder.

First sketch the figure representing this situation.

Where x is the angle of elevation of the ladder.

Let's solve for x.

To solve for x, apply the Trigonometric ratio formula for cosine.

`\cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}}`

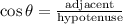
Where:

• Adjacent side is the side adjacent to the angle x = 4.5

,

• Hypotenuse is the longest side = 7

,

• θ is the angle = x

Hence, we have:

`\cos x=(4.5)/(7)`

Take the cos inverse of both sides:

`\begin{gathered} x=\cos ^(-1)((4.5)/(7)) \\ \\ x=49.9\approx50^o \end{gathered}`

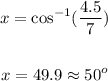
Therefore, the angle of elevation of the ladder is 50 degrees.

ANSWER:

c. 50 degrees