Question

Which pair of functions are inverse functions?()=3+5f(x)=3x+5and()=−3−5g(x)=−3x−5 ()=−+57f(x)=−x+57and()=−7+5g(x)=−7x+5 ()=−3−57f(x)=−3x−57and()=3+57g(x)=3x+57 ()=3−5f(x)=3x−5and()=−53

Answer 1

`\begin{gathered} \mathbf{f(x)=(-x+5)/(7)} \\ \mathbf{g(x)}=f^(-1)(x)=\mathbf{-7x+5} \end{gathered}`

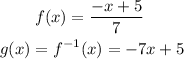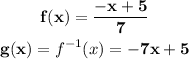
1) Let's examine the f(x) functions and find the inverse function of f(x), in the first pair of functions:

a) At first, let's swap x for y in the original function

`\begin{gathered} f(x)=3x+5 \\ y=3x+5 \\ x=3y+5 \\ -3y=-x+5 \\ 3y=\text{ x-5} \\ (3y)/(3)=(x-5)/(3) \\ y=(x-5)/(3)\text{ } \\ f^(-1)(x)=(x-5)/(3) \end{gathered}`

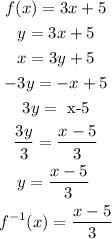
Note that after swapping x for y, we can isolate y on the left side. So as regards g(x) this is not the inverse function of f(x)

2) Similarly, let's check for f(x)

`\begin{gathered} f(x)=(-x+5)/(7) \\ y=(-x+5)/(7) \\ x=(-y+5)/(7) \\ 7x=-y+5 \\ y=-7x+5 \\ f^(-1)(x)=-7x+5 \end{gathered}`

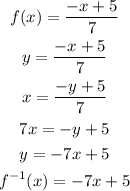
Note that in this case, we can state that these are inverse functions

`f^(-1)(x)=g(x)`

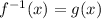
3) Finally, let's find out the last pair of functions.

`\begin{gathered} f(x)=(-3x-5)/(7) \\ y=(-3x-5)/(7) \\ x=(-3y-5)/(7) \\ 7x=-3y-5 \\ 3y=-7x-5 \\ f^(-1)(x)=(-7x-5)/(3) \end{gathered}`

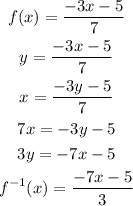
So in this pair, g(x) is not the inverse function of f(x).

4) Hence, the answer is following pair:

`\begin{gathered} f(x)=(-x+5)/(7)\text{ } \\ g(x)=f^(-1)(x)=-7x+5 \end{gathered}`